A man was walking in a forest one day, and he met a woodcutter. It was a hot day, and he sat down for a smoke and engaged in friendly banter with the woodcutter - things about the weather and such. 5 Marlboros later, he asked, "Mr. Woodcutter, you've been making little progress on chopping down the tree the last half hour. Perhaps your axe is too blunt, why don't you sharpen it?"
"That's the truth! The axe has not been sharpened for a long while now, I could make far better progress with a sharp axe!" said the woodcutter.
"Then why not you take some time to sharpen it now? You'd make good progress!" said the man.
"I don't really have time for that, you know. I gotta chop down all these trees, I don't have the luxury of sharpening my axe," replied the woodcutter.
Everybody I know identifies with this story to some degree, and I see a good number people I know, including myself, in the shoes of the woodcutter at times. What is perfectly clear is this: the axe would eventually have to be sharpened or it will be blunted to such an extent that even minimal progress will be impossible. Questions abound: When do we need to sharpen the axe? How many times do we sharpen? Would a partial sharpening do, or do we need to sharpen it to full keeness?
The principle is clear to me - just sharpen the axe sufficiently, as an when would serve to accomplish your work in the minimum time, with minimal effort expended since effort per unit time is assumed a constant. Draw a crucial distinction between work and effort - work is what you're tasked to do, effort is that which you expend to perform the work.
Abraham Lincoln suggested that 60% of the time budget for chopping down a tree should be spent sharpening it. Well, I did an Excel simulation using the solver tool, and the optimal sharpening/chopping schedule is in the chart below.
Assume that it takes 3 times faster to sharpen an axe than it takes to blunt it in normal chopping. That's a reasonable assumption, I think, considering that a sharpening tool is way more abrasive than wood. Also assume that the chopping power of an axe is directly proportional to the sharpness of the axe, and that the axe gets blunted linearly with respect to time.
Spreadsheet source here.
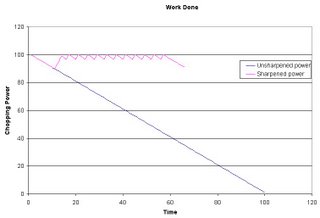
The areas bounded by the coloured lines and the axes represents the total work done (not effort expended). Both areas are equal. This graph illustrates the time taken to achieve a set quantity of work (in this case, 5000 work units)
The blue line - it takes a woodcutter 100 hours to cut down his quota of trees if he doesn't sharpen his axe. The pink line - it takes the same woodcutter 67 hours to cut down the same quota of trees including a total of 14 hours sharpening his axe, at interspersed intervals, during which no work is done chopping trees.
After 1000 iterations Excel's solver plugin threw at the problem, it recommended to sharpen the axe to its maximum sharpness, as soon as it becomes blunt enough to warrant sharpening. You see those wavy lines? That's when the axe gets sharpened.
I didn't expect this result - in fact I was at a total loss on how the results would be like. I'm not good at mathematics, so I could not get an elegant formula and cancel out as many variables as possible, so I had to resort to a numerical simulation model.
The Excel simulation astounded me. If it's right - we HAVE to keep our tools at a maximum state of performance, and maintain as often as possible. I played with the numbers, and if the axe is allowed to deteriorate further before sharpening than is shown in the chart, you'd have to spend more hours sharpening and thus more time to complete the task. So if you leave an axe to blunt to 70% of its maximum sharpness, and then spend time sharpening it to 100% again, you'd spend more than 67 hours cutting the trees.
Real life is way more complex than this thought exercise - one of the applications of this finding to real life is a deriviative where the `maximum sharpness' is the baseline relative competency when you started work, and `degradation of sharpness' happens when technology changes and new tools come online for other people and you didn't keep up. To work in the most efficient way possible, you'd have to learn every genuine productivity booster which comes online. You can't discount anything.
At least this makes me feel better about my compulsion to try out all the new stuff which comes along which have a chance to shave a few seconds off my work. It's mathematically proven to be the most desired form of behaviour by my employer.
No comments:
Post a Comment